Parent Support-for teachers

as you provide support to parents consider their feelings

INTIMIDATED

Learning math in a totally different way means they don't believe they can be helpful.

WORRIED

Anxious that their children will fail because of them

Frustrated

Felling unintelligent and incompetent when unable to do 'second-grade homework'

Confused

Rarely see anything familiar to them. feels like speaking different languages.

Credit: Dr. Hillary Kriesberg

how can you help?

Teachers, here is how you can help parents support their children at home.

We did a Facebook Live on this topic. View the video above and the resources below.

Share the learning trajectories

• Inquiry Path
• Learning the progression of Algorithms
• Family Letters
• Research / Math Background

Help with vocabulary

•Share the glossary
•Share home letters

Educate

•Share "how to help with home" documents
•Share common strategies/methods

•Share exemplars

Glow & Glow

Learn how to effortlessly share student data and progress with families during parent/teacher conferences.

Access Parent's Place Online

Currently, Parent's Place is accessible online, on Think Central. Teachers can access it through their account, and if assigned in the admin section, students can also access it via their accounts.

Many districts have done work to help parents know where to access unit support. See this document from Jordan School district.

See the video explanation for more info on how to access.
(Teachers, on think central, you can click the header 'resources' and the icon will be on that next page.)

2026 Update: Think Central is migrating to a platform called FLIGHT. At this time, we do not have updated information to share.

How to Help at Home

Here are some helpful guiding questions when helping students at home. The parent goal is to ensure students are still carrying the heavy load of thinking and doing. Getting the problem 'right' is not the goal. Understanding how to problem solve, what to do when they don't know, and trying what they 'think' will work is the goal. Homework is a way for students to practice. If you help students get all of the answers right, but students still can't do problems on his/her own, then parent help was not helpful. If they don't know how to do the work or the problems, this is good information for the teacher. Parents can help their student, but should be encouraged to let the teacher know they were unable to be independent. This is not a bad thing. This is exactly the information the teacher needs.

Accessible Algorithms link

Math Expressions includes multiple researched based algorithms for most operations (addition, subtraction, multiplication, and division). Each algorithm presented helps children move closer and closer towards what most of us know as the U.S. Shortcut method, often nicknamed the 'traditional' method. Skipping straight to the traditional method often means students have memorized steps, but don't really understand what they are doing or why. This often makes place value or number sense issues worse.

How to Study Your Math Facts at Home

Evidence shows the more students combine conceptual understanding with fluency practice, the more automatic with facts they will become.

For students in grades 3-5, use this sheet to help practice unknown facts. Stick to one sub-fact (like 5s) and see which multiplication and division facts they don't know. Apply these four steps to those unknown facts..

Family Letters!

Read them! These should come home at least one time each unit, sometimes multiple times. They are a great way to get a snapshot of what might feel new to the parent and what might feel new to the student. They often explain vocabulary and methods you can use to help the child at home.

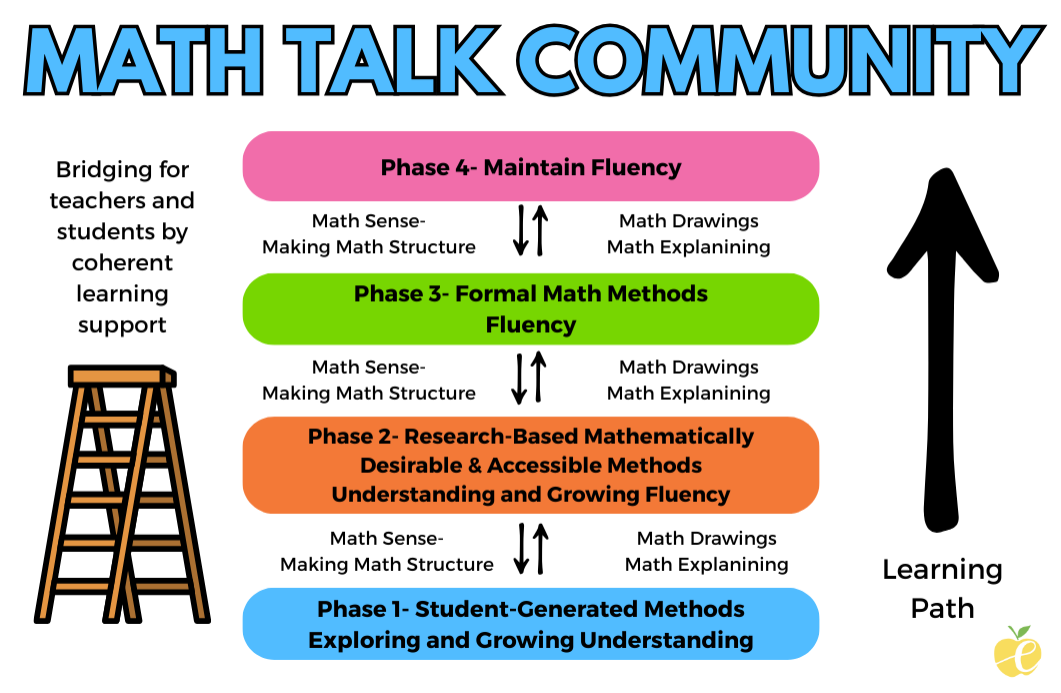
math talk community

Bridging for teachers and students by coherent learning supports and Learning Path

Inquiry Learning Path

Students might come to us being in any of the phases. Our job is to ensure they have built a solid foundation of understanding before releasing them to just practice a bunch of problems. We want your children to be effective, efficient, and flexible. Trust the process. They WON'T be drawing pictures forever! Phase 1 is where we see what students would naturally do with a problem. Students already have math intuition and often how they'd do a problem without our help or how they start a problem helps us to know what skills they bring to the table and how we can best connect what they know to where they need to go. We don't want them to struggle forever, but we do what them to know what it feels like to have a little bit of productive struggle and to believe THEY CAN approach problems they haven't learned yet.

Phase 2

This phase is where we connect what they come up with to the researched-based algorithms we know will help build a strong foundation and help us get to efficient methods. In this phase, we connect, teach explicitly the methods, and ensure students can draw and explain (the why and the how) of their process.

phase 3

In this phase, students formalize methods and become proficient and procedurally fluent. They practice and do enough problems to know what to do without having to think much about it. They don't necessarily need to become fluent with every method, but we look to the standards to decide what methods are necessary at this grade. Just because 'we were taught that way when we were in school' doesn't mean it is the goal of the student in their current grade. Most likely, the method we were taught is ALSO included in the methods your student is learning, but it may not be the standard for their particular grade level. Your teacher may be asking your child to still draw pictures or do other methods to ensure they have a depth of understanding and aren't just memorizing steps.

phase 4

In this phase, we are ensuring students do not forget what they have learned and that they are truly procedurally fluent. We accomplish this through our daily math routines and the 'remembering' side of their homework. We spiral review all of the skills we've learned so far so that we can commit the learning to long-term memory.